Página
Tema 2.1 - Métricas de Error
Resumen
Existen diferentes métricas de error que se pueden aplicar en un problema de regresión para obtener la función f(x) ideal. (Jaume Miralles, 2020)
Las más comunes o habituales y sus definiciones matemáticas son:
1. Error cuadrático medio, mean square error (MSE).
2. Error absoluto medio, mean absolute error (MAE).
3. Raíz del error cuadrático medio, root mean square Error (RMSE).
4. Logaritmo de la raíz del error cuadrático medio, root mean logarithmic square error (RMLSE).
Error Cuadrático Medio (MSE).
El error cuadrático medio o mean square error en inglés (MSE) (Pilar González, 1990), se define como la media de la diferencia entre el valor real y el valor predicho o estimado al cuadrado:
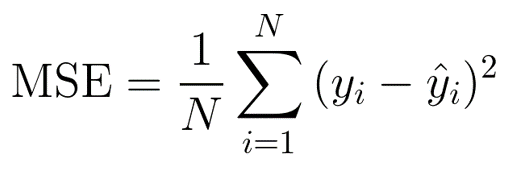
Error Absoluto Medio (MAE).
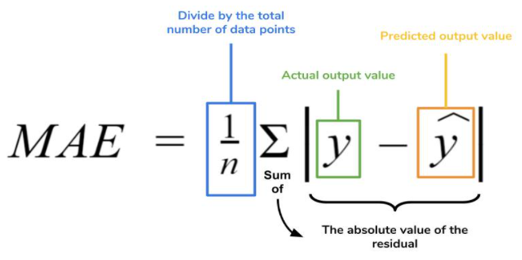
El error absoluto medio o mean absolute error en inglés (MAE)
(Peña, 2007), se define como la diferencia en valor absoluto entre el valor real y el valor predicho:
Raíz del Error Cuadrático Mmedio (RMSE)
La raíz del error cuadrático medio o root mean square Error en inglés (RMSE)
(Raquel Flórez López), se define como la raíz cuadrada de la media de la diferencia entre el valor real y el valor predicho o estimado al cuadrado.
Esta métrica comparada con el error absoluto medio (MAE) amplifica y penaliza los errores grandes. Por otro lado, en MAE cada error contribuye al total del error en función de su valor absoluto.
El siguiente código muestra un ejemplo de cálculo en Python:
Última modificación: viernes, 30 de diciembre de 2022, 23:45