Página
Tema 1.2 - Regresión Lineal
Resumen
Los algoritmos de regresion lineal son los primeros utilizados para este tema de estudio. A contiunuación, se muestran tres imagenes que evidencian el comportamiento de las ventas para tres medios de publicidad en un determinado tiempo .
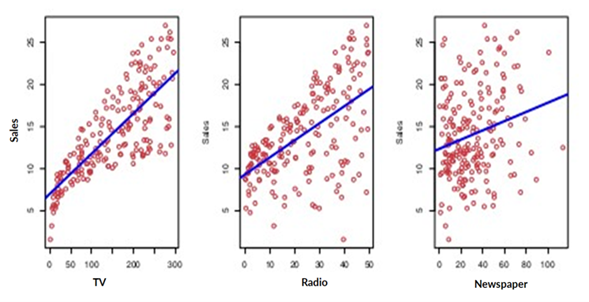
El gráfico muestra las ventas en unidades de miles en función del gasto en TV, radio y periódico en miles de dólares para 200 mercados diferentes. La línea azul representa un modelo simple que se puede utilizar para predecir las ventas utilizando cada una de estas variables.
Es posible determinar cada uno de los valores del eje y en función del eje x utilizando cada una de las gráficas de forma independiente, o bien combinar las tres para obtener una ecuación para las ventas obtenidas en función de las tres entradas. (E. Carbonell, 2020)
𝑆𝑎𝑙𝑒𝑠 ≈ 𝑓 (𝑇𝑉, 𝑅𝑎𝑑 i𝑜 , 𝑁𝑒𝑤𝑠𝑝𝑎𝑝𝑒𝑟)
Lo cual se puede definir utilizando notación vectorial de la siguiente forma:
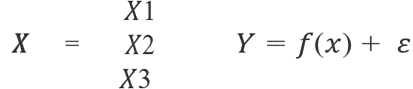
Supongamos que estamos en un plano de dos dimensiones. Se define como función f(x) ideal a la curva que mejor aproxima los puntos.
Supongamos que tenemos una situación como la de la gráfica de abajo:
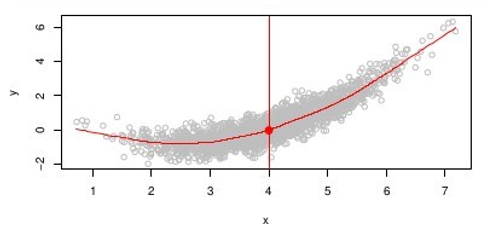
La función de regresión pintada en color rojo sobre la nube de puntos, es donde se observa la de existencia diversos valores de y para un mismo valor del eje x.
Supongamos que queremos obtener el valor de y en el punto x=4,
¿Qué sucede?
Tenemos varios puntos con valores de y diferentes para el punto x=4.
Este valor en el punto x=4 se define de la siguiente forma:
𝑓 (4) = 𝐸 (𝑌|𝑋 = 4)
A la función f(x) ideal también se la conoce con el nombre de Función de Regresión, la cual para todos los puntos del eje x se define de la siguiente forma:
𝐹( 𝑥) = 𝐸 (𝑌 | 𝑋 = 𝑥)
Esta función también se encuentra definida para un vector de x:
𝑓( 𝑥) = 𝑓 (𝑥 1, 𝑥2, 𝑥3) = 𝐸 (𝑌 | 𝑋1 = 𝑥1, 𝑋2 = 𝑥 2, 𝑋3 = 𝑥3)
La función predictora óptima de y es aquella con un error cuadrático medio (MSE) menor:
𝑓( 𝑥) = 𝐸 (𝑌 | 𝑋 = 𝑥)
Última modificación: viernes, 6 de enero de 2023, 15:58